The concepts of rotation and angular momentum are ubiquitous across quantum physics and chemistry, whether one deals with accuracy of atomic clocks, lifetimes of unstable nuclei, or pathways of molecular reaction dynamics. As opposed to translations, quantum rotations are described by non-Abelian SO(3) algebra and possess a discrete spectrum of eigenvalues. This results in a tremendous complexity of the angular momentum properties even for a few interacting particles, such as electrons filling an atomic shell or protons and neutrons arranging themselves into a nucleus.
What happens if one has to deal with angular momentum properties of “real” many-body systems, where the number of interacting particles is infinite?
 The problem seems almost intractable at first glance. It turns out, however, that one can achieve a lot of progress if one looks at the problem from the right perspective, namely, that of quasiparticles. A novel quasiparticle that we have recently introduced is called the “angulon” and consists of a quantum rotor dressed by a field of many-body excitations.
The problem seems almost intractable at first glance. It turns out, however, that one can achieve a lot of progress if one looks at the problem from the right perspective, namely, that of quasiparticles. A novel quasiparticle that we have recently introduced is called the “angulon” and consists of a quantum rotor dressed by a field of many-body excitations.
We have demonstrated that angulons are formed in experiments on molecules in superfluid helium nanodroplets. The angulon, however, can form out of any other impurity whose orbital angular momentum is perturbed by a many-particle environment. It can be, for example, a Rydberg atom or an alkali dimer immersed in an ultracold Bose or Fermi gas, as well as a p-, d-, or f-shell electron interacting with lattice phonons in a crystal. Moreover, angulons can be used as elementary building blocks to understand angular-momentum properties of complex strongly-correlated systems.
The main focus of our group’s research is to understand the properties of angulons and use that knowledge to explain state-of-the-art experiments, as well as to predict novel, previously unobserved phenomena. Below we describe a few recent highlights from our work.
An accessible introduction to angulons can be found in our recent tutorial chapter:
M. Lemeshko, R. Schmidt.
Molecular impurities interacting with a many-particle environment: from ultracold gases to helium nanodroplets, in “Cold Chemistry: Molecular Scattering and Reactivity Near Absolute Zero,” eds. A. Osterwalder and O. Dulieu, Royal Society of Chemistry (2017); arXiv:1703.06753
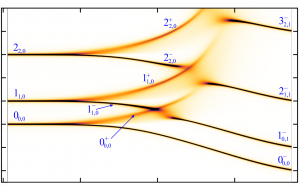 The angulon quasiparticle was first introduced to describe an ultracold molecule coupled to a weakly-interacting Bose-Einstein Condensate (BEC). We approached the problem by constructing a variational and diagrammatic theory which takes into account single-phonon excitations. It turned out that already at this level, sharing of angular momentum between the impurity and bath results in a rich rotational spectrum, featuring “many-body-induced fine structure.” Up to our knowledge, such an effect is absent in any other impurity problem (such as polaron or spin-boson), or in isolated atoms and molecules.
The angulon quasiparticle was first introduced to describe an ultracold molecule coupled to a weakly-interacting Bose-Einstein Condensate (BEC). We approached the problem by constructing a variational and diagrammatic theory which takes into account single-phonon excitations. It turned out that already at this level, sharing of angular momentum between the impurity and bath results in a rich rotational spectrum, featuring “many-body-induced fine structure.” Up to our knowledge, such an effect is absent in any other impurity problem (such as polaron or spin-boson), or in isolated atoms and molecules.
R. Schmidt, M. Lemeshko. Rotation of quantum impurities in the presence of a many-body environment,
Phys. Rev. Lett. 114, 203001 (2015), arxiv:1502.03447
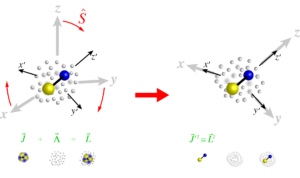 The approach described above assumed that the impurity-bath interactions are weak enough such that only one phonon can be excited at a given time. If the coupling gets stronger, however, multiple phonon excitations will take place. Since each phonon carries angular momentum, in the limit of strong interactions one has to deal with Wigner 3nj-symbols of infinite order n, which renders the problem (seemingly) intractable.
The approach described above assumed that the impurity-bath interactions are weak enough such that only one phonon can be excited at a given time. If the coupling gets stronger, however, multiple phonon excitations will take place. Since each phonon carries angular momentum, in the limit of strong interactions one has to deal with Wigner 3nj-symbols of infinite order n, which renders the problem (seemingly) intractable.
Recently we have introduced a novel canonical transformation, which allows to eliminate complex angular momentum algebra from the angulon problem. The transformation made it possible to solve the problem exactly in the limit of a non-rotating impurity, where an infinite number of phonon excitations are involved. Furthermore, the transformation singles out good quantum numbers of the problem — such as total angular momentum — which is crucial to achieve a general understanding of the underlying physics.
R. Schmidt, M. Lemeshko. Deformation of a quantum many-particle system by a rotating impurity,
Phys. Rev. X 6, 011012 (2016), arXiv:1507.03987
Chemical physicists routinely trap molecules inside nanodroplets of superfluid 4He, sometimes called ‘nanocryostats.’ In such a way, molecules are cooled down to ~0.4 Kelvin and are perfectly isolated from external perturbations, which allows to perform very accurate spectroscopic measurements.
While superfluid helium does not cause a substantial broadening of molecular spectral lines, it affects molecular rotation. In particular, molecules in superfluid helium acquire an effective moment of inertia, that is larger compared to its gas-phase value. This effect is somewhat similar to renormalization of the effective mass for polarons — electrons interacting with a crystal lattice.
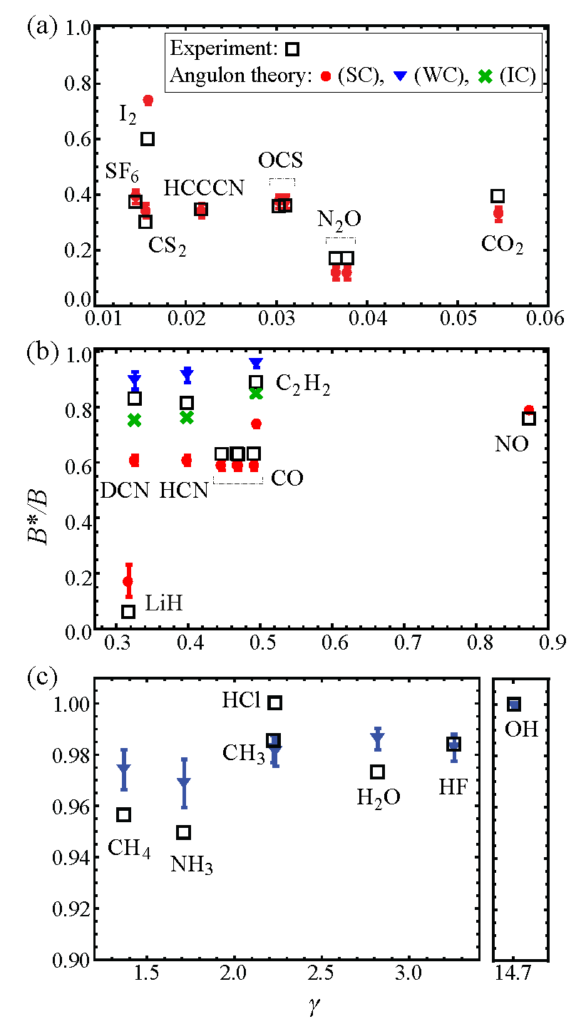
Understanding molecular rotation in superfluid 4He represents a formidable challenge and usually requires extensive numerical simulations, e.g. those based on path-integral, variational, and diffusion quantum Monte-Carlo algorithms. Recently we have demonstrated that the problem can be simplified tremendously if one assumes that molecules in superfluid helium form angulons and thereby tackles the problem from the quasiparticle perspective.
Figure on the right compares the results of the angulon theory in the Strong Coupling (SC), Weak Coupling (WC), and Intermediate Coupling (IC) regimes with Experiment.
Such a good agreement with experiment provides strong evidence of angulon formation inside superfluid helium nanodroplets. Furthermore, within the angulon theory, the effective rotational constants can be obtained as straightforward analytic solutions of a simple microscopic Hamiltonian, and provided with a transparent physical interpretation.
Aside from explaining experiments on molecules in superfluid helium, these results pave the way to understanding molecular rotations in other liquid in solid phases in terms of angulons.
M. Lemeshko. Quasiparticle approach to molecules interacting with quantum solvents,
Phys. Rev. Lett. 118, 095301 (2017); Physics 10, 20 (2017)
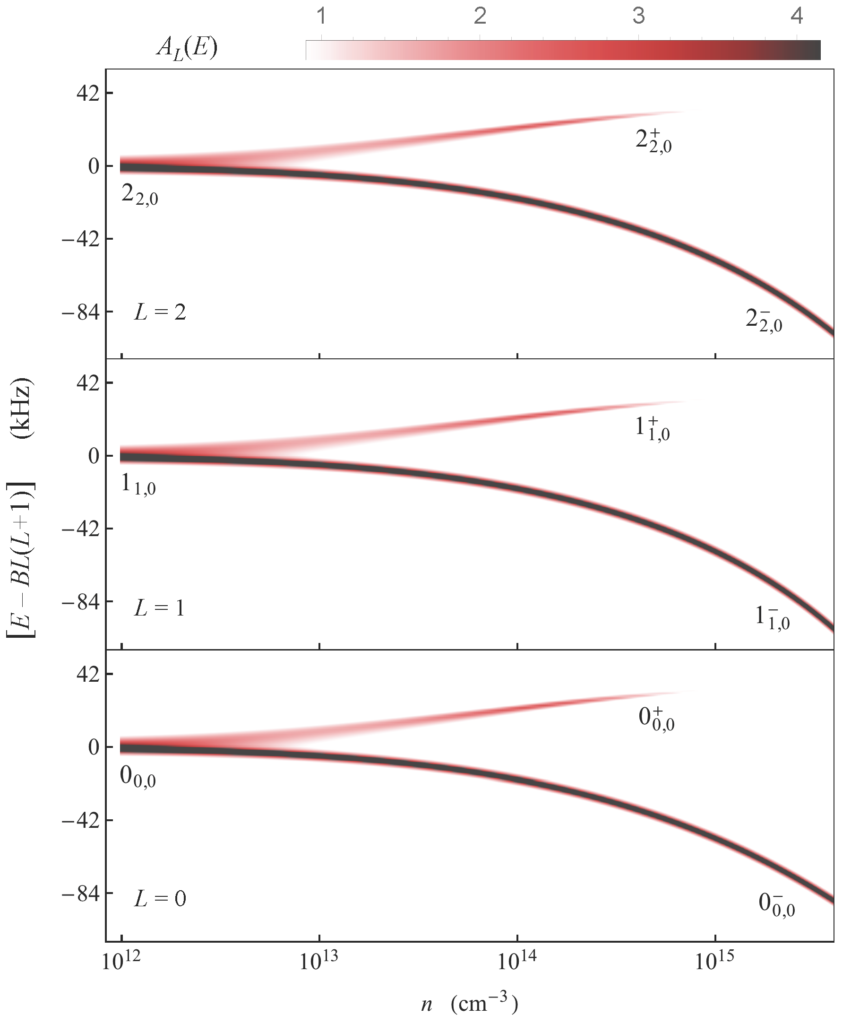 We have shown that the angulon physics can be observed even for weakly-interacting systems available in experiment, such as cold molecules interacting with ultracold quantum gases.
We have shown that the angulon physics can be observed even for weakly-interacting systems available in experiment, such as cold molecules interacting with ultracold quantum gases.
First of all, we developed a pseudopotential approach which allows to incorporate realistic ab initio potential energy surfaces into the angulon calculations. Then, based on such accurate potentials, we evaluated the Rotational Lamb Shifts for the CN— anion in Bose-Einstein Condensates of Rb and Sr, and found it large enough to be detected in state-of-the-art experiments (see Figure on the right).
B. Midya, M. Tomza, R. Schmidt, M. Lemeshko
Rotation of cold molecular ions inside a Bose-Einstein condensate,
Phys. Rev. A 94, 041601 (2016) (Rapid Comm.), arXiv:1607.06092
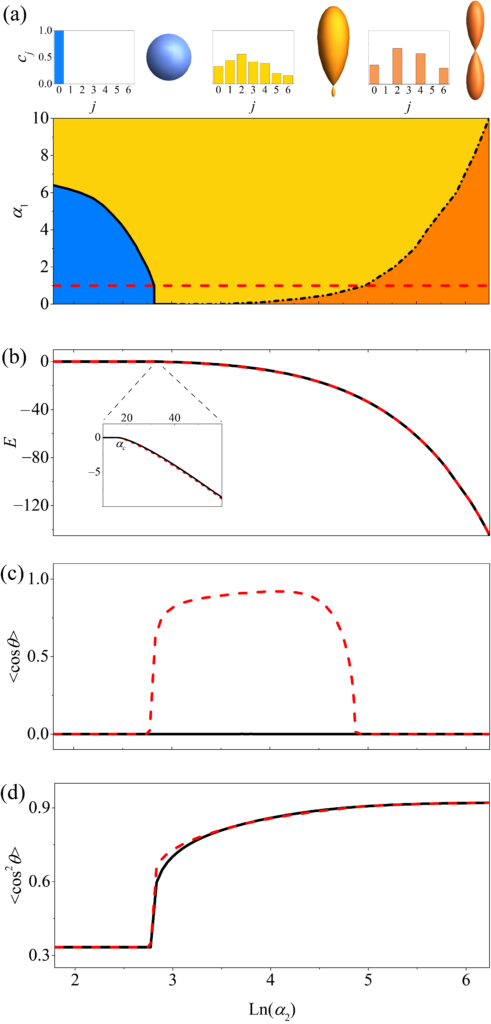 In 1933 Landau predicted that electrons moving through crystals can undergo a ‘self-localization transition.’ The latter takes place when the electron-induced distortion of the crystal lattice is strong enough to affect the motion of the electron itself, confining its wavefunction in space. The existence of the self-localization transition in polarons has been under an active debate ever since.
In 1933 Landau predicted that electrons moving through crystals can undergo a ‘self-localization transition.’ The latter takes place when the electron-induced distortion of the crystal lattice is strong enough to affect the motion of the electron itself, confining its wavefunction in space. The existence of the self-localization transition in polarons has been under an active debate ever since.
Recently, we have shown that for angulons a self-localization transition takes place already at the mean-field level of theory. Furthermore, due to the various symmetries of the impurity-bath interactions that can take place, the resulting localization behavior of angulons is substantially richer than for polarons, and features a few distinct self-localized states.
An example of a ‘localization diagram’ is shown in panel (a) of the Figure. Blue corresponds to a delocalized ground state, yellow — to an oriented ground state (indefinite parity), while orange — to an aligned ground state (definite parity). Panels (b)-(d) show the dependence of the ground-state energy, as well as orientation and alignment cosines.
X. Li, R. Seiringer, M. Lemeshko.
Angular self-localization of impurities rotating in a bosonic bath, Phys. Rev. A 95, 033608 (2017), arXiv:1610.04908
It is a common knowledge that an effective interaction of a quantum impurity with an electromagnetic field can be screened by surrounding charge carriers, whether mobile or static. We have demonstrated that very strong, anomalous screening can take place in the presence of a neutral, weakly-polarizable environment, due to an exchange of orbital angular momentum between the impurity and the bath. Furthermore, we show that it is possible to generalize all phenomena related to isolated impurities in an external field to the case when a many-body environment is present, by casting the problem in terms of the angulon quasiparticle. As a result, the relevant observables such as the effective Rabi frequency, geometric phase, and impurity spatial alignment are straightforward to evaluate in terms of a single parameter: the angular-momentum-dependent screening factor.
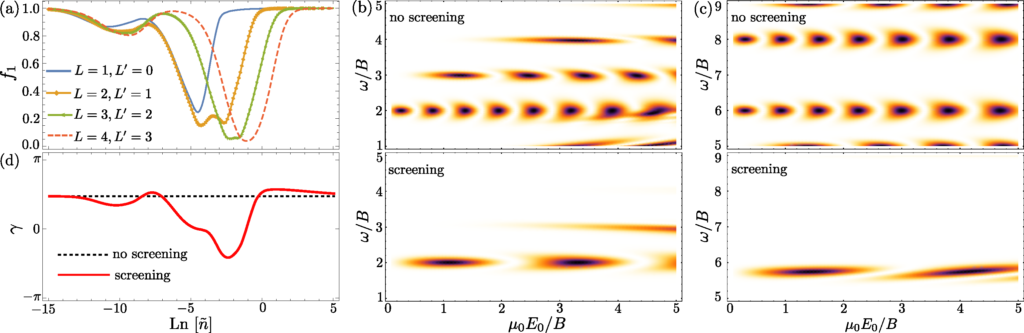
E. Yakaboylu, M. Lemeshko. Anomalous screening of quantum impurities by a neutral environment,
Phys. Rev. Lett. 118, 085302 (2017), arXiv:1612.02820
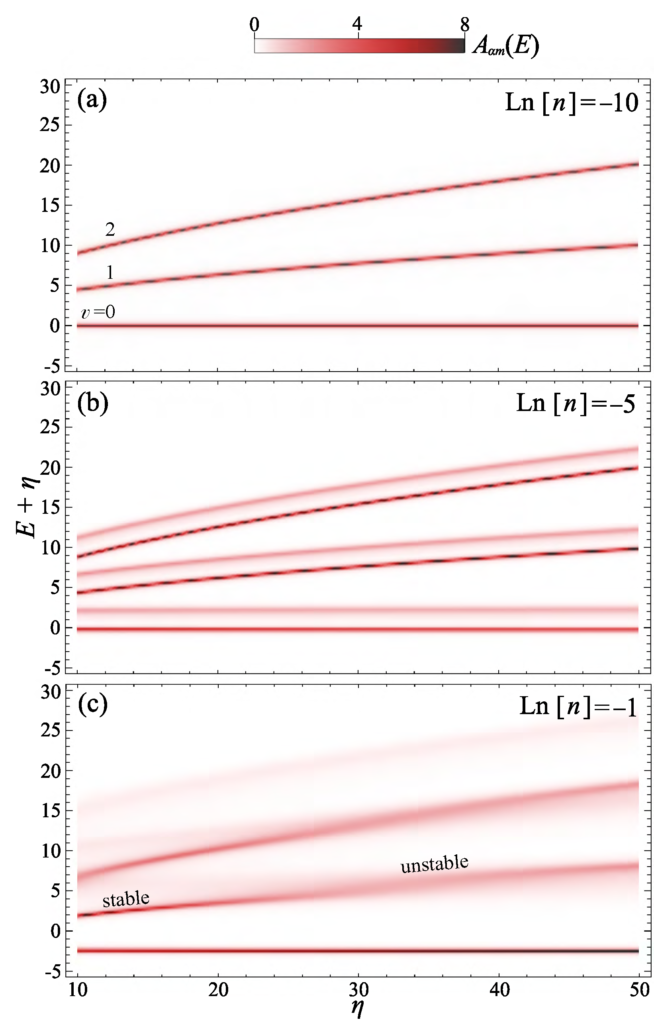 When molecules are placed in external electromagnetic fields, their properties — even in the gas phase — change dramatically. A field breaks rotational symmetry, thereby altering spectroscopic selection rules and molecular collision outcomes.
When molecules are placed in external electromagnetic fields, their properties — even in the gas phase — change dramatically. A field breaks rotational symmetry, thereby altering spectroscopic selection rules and molecular collision outcomes.
Things become even more intriguing in the presence of a quantum many-body bath. Here, we have considered the angulon problem in the presence of an intense electrostatic field. It turned out that in such conditions angulons turn into pendulons — quantum spherical librators dressed by a field of phonon excitations.
For pendulons, there occur new instabilities accompanied by the angular momentum transfer between the impurity and the bath. Moreover, the field can be used as an additional knob to tune the instabilities’ positions in the spectrum. This paves the way to a precise control of angular momentum transfer in many-particle systems.
E. S. Redchenko, M. Lemeshko
Libration of strongly-oriented polar molecules inside a superfluid, Chem. Phys. Chem 17, 3649 (2016), arXiv:1609.08161
